Access answers to Maharashtra Board Solutions For Class 8 Maths Part 1 Chapter 1 Rational and Irrational Numbers

Practice set 1.1 PAGE NO: 02

1. Show the following numbers on a number line. Draw a separate number line for each example.

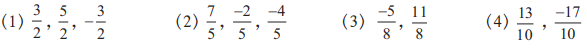
Solution:

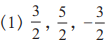
Here, the denominator of each fraction is 2.

∴ Each unit will be divided into 2 equal parts.

Here, the denominator of each fraction is 5.

∴ Each unit will be divided into 5 equal parts.

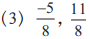
Here, the denominator of each fraction is 8.

∴ Each unit will be divided into 8 equal parts.

Here, the denominator of each fraction is 10.

∴ Each unit will be divided into 10 equal parts.

2. Observe the number line and answer the questions.

(1) Which number is indicated by point B?
(2) Which point indicates the number 1 ¾?
(3) State whether the statement, ‘the point D denotes the number 5/2, is true or false.

Solution:

We know that, each part between integers is divided into 4 parts on the number line

So, each part equals ¼.

(1) Which number is indicated by point B?

Point B is marked on the 10th equal part on the left side of O (i.e., the negative side).

∴ The number indicated by point B is −10/4.

(2) Which point indicates the number 1 ¾?

1 ¾ can be represented as:

Point C is marked on the 7th equal part on the right side of O.

∴ The number 1 ¾ is indicated by point C.

(3) State whether the statement, ‘the point D denotes the number 5/2, is true or false.

The statement is true.

Point D is marked on the 10th equal part on the right side of O.

∴ D denotes the number 10/4 = (5 × 2) / (2 × 2) = 5/2

Practice set 1.2 PAGE NO: 03

1. Compare the following numbers.

Solution:

(1) -7, -2

Now if there are two numbers, a and b such that a >b then

-a <-b.

Since, 7 >2

∴ – 7 <-2

(2) 0, -9/5

Since, -9/5 is a negative quantity; it will always be less than zero.

∴ 0 >-9/5.

(3) 8/7, 0

Since, 8/7 is a positive quantity; it will always be greater than zero.

∴ 0 <8/7.

(4) -5/4, ¼

Since the denominators are same, we shall check which number in the numerator is greater.

-5 <1

∴ -5/4 <¼

(5) 40/29, 141/29

Since the denominators are same, we shall check which number in the numerator is greater.

40 <141

∴ 40/29 <141/29

(6) -17/20, -13/20

Now if there are two numbers, a and b such that a >b then

-a <-b.

Since, 17 >13

So, -17 <-13.

Now, the denominator is same, we shall check which number in the numerator is greater.

Since, -17 <-13

∴ -17/20 <-13/20

(7) 15/12, 7/16

Firstly let us make the denominators equal.

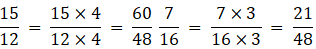
Now the denominators are equal, we shall check whose numerator is greater.

60 >21.

∴ 15/12 >7/16

(8) -25/8, -9/4

Firstly let us make the denominators equal.

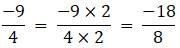
Now the denominators are equal, we shall check whose numerator is greater.

-25 <-18.

∴ -25/18 <-9/4

(9) 12/15, 3/5

Firstly let us make the denominators equal.

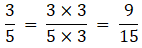
Now the denominators are equal, we shall check whose numerator is greater.

12 >9.

∴ 12/15 >3/5

(10) -7/11, -3/4

Firstly let us make the denominators equal.

Now the denominators are equal, we shall check whose numerator is greater.

-28 >-33.

∴ -7/11 >-3/4

Practice set 1.3 PAGE NO: 04

1. Write the following rational numbers in decimal form.

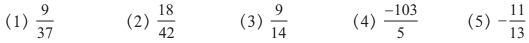
Solution:

(1) 9/37

Let us divide the fraction using long-division method.

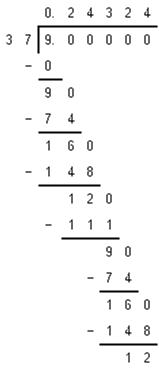
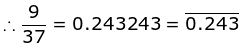
(2) 18/42

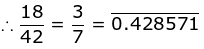
(3) 9/14

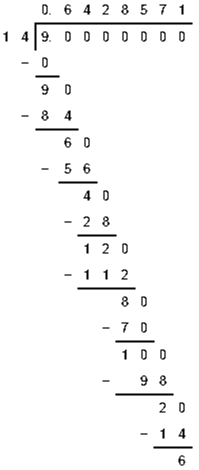
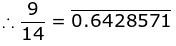
(4) -103/5

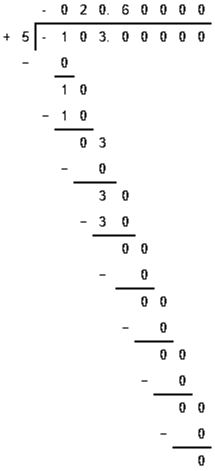
∴ -103/5 = -20.6

(5) -11/13

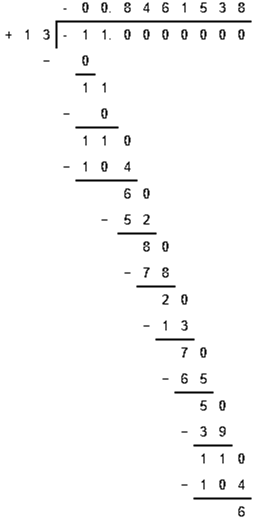
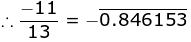
Practice set 1.4 PAGE NO: 05

1. The number √2 is shown on a number line. Steps are given to show √3 on the number line using √2. Fill in the boxes properly and complete the activity.

Activity:
● The point Q on the number line shows the number …….
● A line perpendicular to the number line is drawn through the point Q.
Point R is at unit distance from Q on the line.

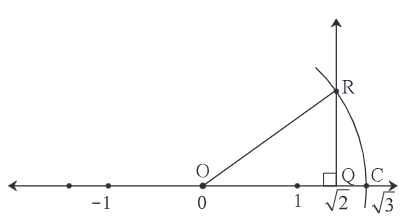
● Right angled ∆ORQ is obtained by drawing seg OR.
● l(OQ) = √2, l(QR) = 1
∴ by Pythagoras theorem,
[l(OR)]² = [l(OQ)]² + [l(QR)]²

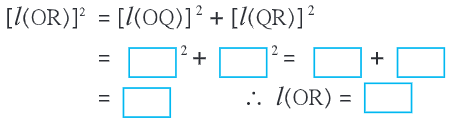
Draw an arc with center O and radius OR. Mark the point of intersection of the line and the arc as C. The point C shows the number √3.

Solution:

● The point Q on the number line shows the number √2.

● A line perpendicular to the number line is drawn through the point Q.

Point R is at unit distance from Q on the line. (Here unit distance means 1 cm or any other unit.)

● Right angled ∆ORQ is obtained by drawing seg OR.

● l(OQ) = √2, l(QR) = 1

∴ By Pythagoras theorem,

[l(OR)]² = [l(OQ)]² + [l(QR)]²

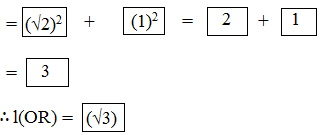
By taking square root on both the sides,

Draw an arc with centre O and radius OR. Mark the point of intersection of the line and the arc as C. The point C shows the number √3.

2. Represent √5 on the number line.

Solution:

Let us draw a number line, mark the center as point O and mark a point Q at number 2 such that it is 2cm from the center i.e., l(OQ) = 2 units.

Now, draw a line QR perpendicular to the number line through the point Q such that l(QR) = 1 unit.

Draw seg OR.

∆OQR formed is a right angled triangle.

By using Pythagoras theorem,

[l(OR)]² = [l(OQ)]² + [l(QR)]²

= 2² + 1²

= 4 + 1

= 5

∴l(OR) = √5 units

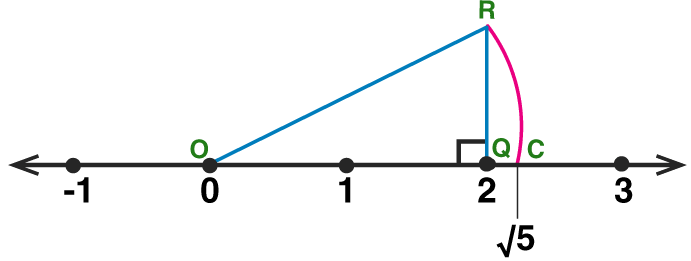
By taking square root on both the sides,

Draw an arc with centre O and radius OR. Mark the point of intersection of the number line and arc as C. The point C shows the number √5.

3. Show the number √7 on the number line.

Solution:

Let us draw a number line, mark the center as point O and mark a point Q at number 2 such that it is 2cm from the center i.e., l(OQ) = 2 units.

Draw a line QR perpendicular to the number line through the point Q such that l(QR) = 1 unit.

Draw seg OR.

∆OQR formed is a right angled triangle.

By using Pythagoras theorem,

[l(OR)]² = [l(OQ)]² + [l(QR)]²

= 2² + 1²

= 4 + 1

= 5

∴ l(OR) = √5 units

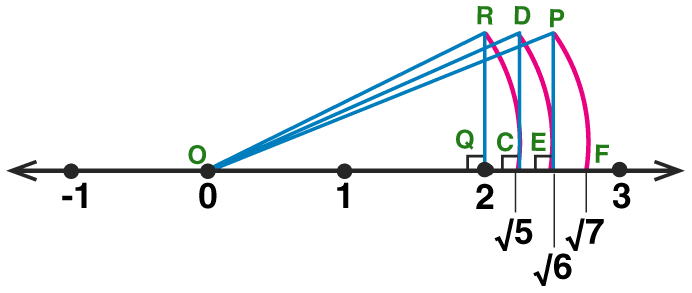
By taking square root on both the sides,

Draw an arc with centre O and radius OR.

Mark the point of intersection of the number line and arc as C. The point C shows the number √5.

Similarly, draw a line CD perpendicular to the number line through the point C such that l(CD) = 1 unit.

By using Pythagoras theorem,

l(OD) = √6 units

The point E shows the number √6 .

Similarly, draw a line EP perpendicular to the number line through the point E such that l(EP) = 1 unit.

By Pythagoras theorem,

l(OP) = √7 units

The point F shows the number √7.